Difference between revisions of "Muscle models"
(→OxP+glycolysis models) |
|||
| (22 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
===Introduction=== | ===Introduction=== | ||
| − | <p align=justify>Skeletal muscle is one of the most abundant tissues in mammals, accounting for up to 40% of the total mass ofthe human body (Janssen et al., 2000)<cite>1</cite>. The contraction–relaxation cycle in muscle requires energy that is mostly generated aerobically by mitochondria particularly abundant in adult muscle fibres. It is worth to note that skeletal muscle can maintain ATP concentration constant during the transition from rest to exercise, whereas metabolic reaction rates may increase substantially (Kunz, 2001) <cite>2</cite>. Although it is well known that skeletal muscle adaptations to exercise depend on duration, intensity, and frequency, changes in muscle proteins associated with different types of exercise have not been well characterized (Gonzalez‐Freire et al., 2017) <cite>3</cite>. Moreover, the quantitative contributions of different fiber types to the energy demand and detailed dynamics of metabolic responses of the skeletal muscle in response to different exercise | + | <p align=justify>Skeletal muscle is one of the most abundant tissues in mammals, accounting for up to 40% of the total mass ofthe human body (Janssen et al., 2000) <cite>1</cite>. The contraction–relaxation cycle in muscle requires energy that is mostly generated aerobically by mitochondria particularly abundant in adult muscle fibres. It is worth to note that skeletal muscle can maintain ATP concentration constant during the transition from rest to exercise, whereas metabolic reaction rates may increase substantially (Kunz, 2001) <cite>2</cite>. Although it is well known that skeletal muscle adaptations to exercise depend on duration, intensity, and frequency, changes in muscle proteins associated with different types of exercise have not been well characterized (Gonzalez‐Freire et al., 2017) <cite>3</cite>. Moreover, the quantitative contributions of different fiber types to the energy demand and detailed dynamics of metabolic responses of the skeletal muscle in response to different exercise |
| − | intensities are unknown. Indeed, accurate measurements to quantify the recruitment and metabolic activation of muscle fibers in vivo have not been possible to date (Li et al., 2012) <cite>4</cite>. So due to a shortage of dynamic in vivo human data, the regulatory mechanisms of functioning of the skeletal muscle metabolism are poorly understood. To quantitatively interpret the limited data, a physiologically based mathematical modeling approach can be applied (Li et al., 2010) <cite>5</cite>.</p> | + | intensities are unknown. Indeed, accurate measurements to quantify the recruitment and metabolic activation of muscle fibers ''in vivo'' have not been possible to date (Li et al., 2012) <cite>4</cite>. So due to a shortage of dynamic ''in vivo'' human data, the regulatory mechanisms of functioning of the skeletal muscle metabolism are poorly understood. To quantitatively interpret the limited data, a physiologically based mathematical modeling approach can be applied (Li et al., 2010) <cite>5</cite>.</p> |
===Published models=== | ===Published models=== | ||
| − | <p align=justify>One of the first theoretical investigation in this field was conducted by Bernard Korzeniewski (Korzeniewski, 1998,1999) <cite>6</cite><cite>7</cite>. He developed the computational model of oxidative phosphorylation (OxP) in skeletal muscle mitochondria in order to decipher a regulatory mechanism of the adjustment of ATP production to ATP consumption in contracting muscle. During the transition from the resting state of muscles to their maximal exercise, there is a great increase in energy demand (ATP consumption). Mitochondrial OxP is the main process responsible for ATP production in | + | |
| − | most muscle fibre types under most conditions. Therefore, mitochondria have to ‘know’ in some way how fast should they produce ATP in a given moment of time to meet the rate of energy consumption and to avoid a drastic decrease in cytosolic phosphorylation potential which would hinder muscle contraction.Two alternative mechanisms of the adjusting the energy (ATP) production rate to the energy consumption rate were postulated. They can be called the ‘negative feedback’ and ‘parallel activation’ (Figure 1).</p> | + | ====Korzeniewski models==== |
| + | <p align=justify>One of the first theoretical investigation in this field was conducted by Bernard Korzeniewski (Korzeniewski, 1998,1999) <cite>6</cite><cite>7</cite>. He developed the computational model of oxidative phosphorylation (OxP) in skeletal muscle mitochondria in order to decipher a regulatory mechanism of the adjustment of ATP production to ATP consumption in contracting muscle. During the transition from the resting state of muscles to their maximal exercise, there is a great increase in energy demand (ATP consumption). Mitochondrial OxP is the main process responsible for ATP production in most muscle fibre types under most conditions. Therefore, mitochondria have to ‘know’ in some way how fast should they produce ATP in a given moment of time to meet the rate of energy consumption and to avoid a drastic decrease in cytosolic phosphorylation potential which would hinder muscle contraction.Two alternative mechanisms of the adjusting the energy (ATP) production rate to the energy consumption rate were postulated. They can be called the ‘negative feedback’ and ‘parallel activation’ (Figure 1).</p> | ||
[[File:Korzeniewski1998 fig1 mechanisms ATP concentration.png|center]] | [[File:Korzeniewski1998 fig1 mechanisms ATP concentration.png|center]] | ||
| Line 37: | Line 38: | ||
| + | ====OxP+glycolysis models==== | ||
<p align=justify>It must be emphasized that the computer model of OxP+glycolysis used in the present study contains several simplifications and approximations. First, a simple linear dependence of the glycolytic flux on [ADP] was extracted from the initial model (Lambeth and Kushmerick, 2002)<cite>8</cite>. This was justified by the fact that the regulation by ADP, AMP and Pi cannot alone account for the kinetic properties of glycolysis in | <p align=justify>It must be emphasized that the computer model of OxP+glycolysis used in the present study contains several simplifications and approximations. First, a simple linear dependence of the glycolytic flux on [ADP] was extracted from the initial model (Lambeth and Kushmerick, 2002)<cite>8</cite>. This was justified by the fact that the regulation by ADP, AMP and Pi cannot alone account for the kinetic properties of glycolysis in | ||
intact muscle. Such a simple description allowed including in the model the direct activation of glycolysis by some contraction-related factor and | intact muscle. Such a simple description allowed including in the model the direct activation of glycolysis by some contraction-related factor and | ||
| Line 42: | Line 44: | ||
<p align=justify>A set of integrated computational model describing different cellular factors (concentration of free ADP, Pi or pH level in the cell) regulating OxP and glycolysis has been developed (Mader, 2003) <cite>13</cite>; (Vinnakota et al., 2006) <cite>14</cite>; (Wu et al., 2007) <cite>15</cite>. Namely, Mader <cite>13</cite> presented a mathematical description of the regulation of ATP production (or the activity of OxP) in muscle cells as a function of (1) free [ADP] as the substrate and (2) a second driving force F*deltaG (kilojoules per mole) resulting from the | <p align=justify>A set of integrated computational model describing different cellular factors (concentration of free ADP, Pi or pH level in the cell) regulating OxP and glycolysis has been developed (Mader, 2003) <cite>13</cite>; (Vinnakota et al., 2006) <cite>14</cite>; (Wu et al., 2007) <cite>15</cite>. Namely, Mader <cite>13</cite> presented a mathematical description of the regulation of ATP production (or the activity of OxP) in muscle cells as a function of (1) free [ADP] as the substrate and (2) a second driving force F*deltaG (kilojoules per mole) resulting from the | ||
| − | difference of free energy deltaG_ox,ap (kilojoules per mole) – deltaG_ATP,cyt (kilojoules per mole), which is necessary to sustain the flow of ATP from inside the mitochondrian to the cytosol. Results from the computational simulations demonstrated a high level of similarity with the experimentally observed dynamic behaviour of measurable parameters of OxP, glycolysis and the behaviour of the parameters of the | + | difference of free energy deltaG_ox,ap (kilojoules per mole) – deltaG_ATP,cyt (kilojoules per mole), which is necessary to sustain the flow of ATP from inside the mitochondrian to the cytosol. Results from the computational simulations demonstrated a high level of similarity with the experimentally observed dynamic behaviour of measurable parameters of OxP, glycolysis and the behaviour of the parameters of the cytosolic high energy phosphate system. Furthermore, the computational simulations showed that complex dynamic behaviour in real biological systems can be ruled by a few general principles and a relatively simple set of equations. It is, however, emphasized by author that the model needs a more detailed implementation of the characteristics of the reactions occurring at the site of the mitochondria. In turn, Vinnakota with co-authors <cite>14</cite> developed the model, which is aimed to explain the influence of pH on biochemical reaction kinetics (Figure 4) and equilibria by prediction of experimental data from the study of Scopes <cite>16</cite> on ''in vitro'' glycogenolysis using a cell free reconstituted enzyme system (Figure 5). They found that a wide range of experimental data, 13 time series out of 15 from three experiments, are explained by adjustment of only three kinetic parameters out of nearly 100 parameters, which leads to a significant conclusion that accurate accounting for the physical chemistry (pH-dependent enzyme kinetics) leads to a model with greater predictive power.</p> |
{| align="center" style="background:#f8f9fa; border:1px solid #c8ccd1; font-size:100%; margin-center:1em" cellspacing=0 cellpadding=0 | {| align="center" style="background:#f8f9fa; border:1px solid #c8ccd1; font-size:100%; margin-center:1em" cellspacing=0 cellpadding=0 | ||
| Line 53: | Line 55: | ||
| − | <p align=justify>Wu and | + | <p align=justify>Wu and co-authors <cite>15</cite> used previously developed model (Figure 6) of mitochondrial oxidative phosphorylation (Beard, 2005) <cite>17</cite> and data from <sup>31</sup>P-nuclear magnetic resonance spectroscopy of human forearm flexor muscle (Jeneson et al., 1993) <cite>18</cite> to test the hypothesis that substrate level (concentrations of ADP and inorganic phosphate) represents the primary signal governing the rate of mitochondrial ATP synthesis and maintaining the cellular ATP hydrolysis potential in skeletal muscle.</p> |
[[File:Wu_etal_2007_fig6_model_scheme.png|center]] | [[File:Wu_etal_2007_fig6_model_scheme.png|center]] | ||
| Line 70: | Line 72: | ||
|} | |} | ||
| − | <span style="font-size:90% | + | <span style="font-size:90%">'''Figure 7 from (Wu et al., 2007)''' <cite>15</cite>. Model prediction of ADP concentration and inorganic phosphate concentration in cytoplasm as a function of ATP hydrolysis rate in the healthy subjects. A: plot of predicted ADP concentration in cytoplasm, [ADP]c, as a function of ATP hydrolysis rate, ATPase flux. B: plot of predicted Pi concentration in cytoplasm, [Pi]c, as a function of ATP hydrolysis rate, ATPase flux. The solid and dashed lines represent model-predicted results. The circles represent experimentally measured estimation from Jeneson et al. <cite>18</cite>. Solid line correspond to the optimal value of the total pool of exchangeable phosphate (TPP) = 36.8 mM; dashed lines correspond to TPP = 40.5 mM (10% greater than the optimal value).</span> |
| + | |||
| + | ====Cabrera models==== | ||
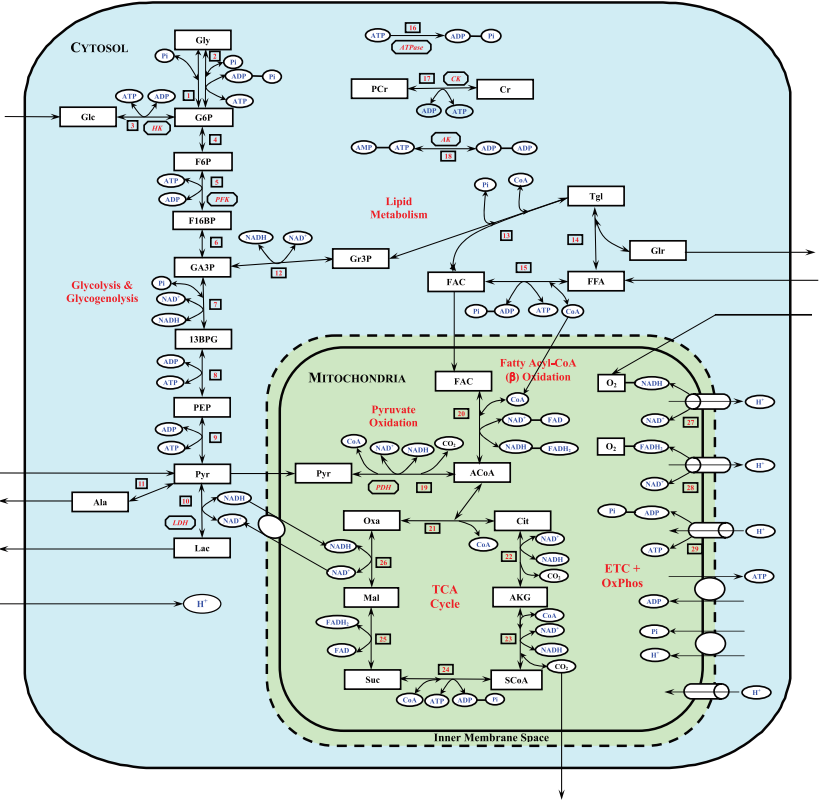
| + | <p align=justify>The mechanistic basis for addressing key questions with respect to the mechanisms of metabolic regulation in contracting skeletal muscle was provided by group of Prof. Marco Cabrera (Case Western Reserve University, Cleveland, Ohio) using a set of developed mathematical models <cite>4</cite>; <cite>5</cite>; <cite>19</cite>; <cite>20</cite>; <cite>21</cite>; <cite>22</cite>; <cite>23</cite>; <cite>24</cite>; <cite>25</cite>; <cite>26</cite>. In particularly, a physiologically based mathematical model of cellular metabolism in perfused skeletal muscle that simulates metabolic responses to moderate intensity exercise (60% V<sub>O2max</sub>) (Li et al., 2009) <cite>26</cite> differs significantly from their previous models of cardiac and skeletal muscle cellular metabolism and other published models of skeletal muscle cellular metabolism in that both the biochemical reactions governing cellular metabolism are considered reversible with their fluxes satisfying Haldane relationships (thermodynamic constraints) and the model incorporates the primary substrates (glucose and free fatty acids (FFAs)) together with key metabolic pathways of cellular metabolism (glycolysis, lipid metabolism, CK, TCA cycle, and oxidative phosphorylation). The model distinguishes metabolic processes occurring in capillary blood, cytosol, and mitochondria and incorporates distinct transport processes between these domains (Figures 8-9).</p> | ||
| + | |||
| + | [[File:Li_etal_2009_fig8_model_scheme.png|center]] | ||
| + | |||
| + | <span style="font-size: 90%"> '''Figure 8 from (Li et al., 2009)''' <cite>26</cite>. Schematic diagram of the structure of the model for blood-tissue cell exchange and cellular metabolism in skeletal muscle. The compartments are assumed to be perfectly mixed, and the capillary blood and tissue interstitial fluid (ISF) domains are assumed to be in phase-equilibrium with each other so that C<sub>isf, ''j''</sub> = C<sub>bl, ''j''</sub> = C<sub>ven, ''j''</sub> for any chemical species ''j''. The tissue cells domain is further compartmentalized into the cytosolic and mitochondrial domains with the chemical species having distinct dynamics in these 2 subcellular domains. A total of 9 species [glucose (Glc), lactate (Lac), pyruvate (Pyr), alanine (Ala), free fatty acid (FFA), glycerol (Glr), CO<sub>2</sub>, O<sub>2</sub>, and H<sup>+</sup> (protons)] undergo bloodcytosol exchange, and 11 species [Pyr, fatty acyl-CoA (FAC), CoA, reduced nicotinamide adenine dinucleotide (NADH), oxidized nicotinamide adenine dinucleotide (NAD<sup>+</sup>), ATP, ADP, inorganic phosphate (P<sub>i</sub>), CO<sub>2</sub>, O<sub>2</sub>, and H<sup>+</sup>] undergo cytosol-mitochondria exchange. </span> | ||
| + | |||
| + | |||
| + | <p align=justify>This comprehensive computational model accounts for proton handling and considers the coupled energy controller pairs ATP-ADP and NADH-NAD<sup>+</sup> as cosubstrates. A key feature of the model is its ability to simulate blood and tissue responses, which are routinely measured in experimental studies, as well as to predict dynamic intracellular species concentrations and reaction rates, which cannot be measured with the currently available experimental techniques. The underlying hypothesis of the model is that during the transition from rest to exercise, the cytosolic redox state is more sensitive to metabolic disturbance than the mitochondrial redox state. This hypothesis was tested by simulating skeletal muscle metabolic responses during moderate intensity exercise [60% maximal O<sub>2</sub> consumption (V<sub>O2max</sub>)] with different transport (shuttling) rates of reducing equivalents (NADH and NAD<sup>+</sup>) between cytosol and mitochondria and different intracellular glycogen concentrations.</p> | ||
| + | [[File:Li_etal_2009_fig9_model_scheme.png|center]] | ||
| + | |||
| + | <span style="font-size: 90%"> '''Figure 9 from (Li et al., 2009)''' <cite>26</cite>. Schematic diagram of biochemical pathways depicting various chemical reactions and species involved in the cellular metabolism of skeletal muscle. The reactions and species are further compartmentalized into the cytosolic and mitochondrial reactions and species. Gly, glycogen; G6P, glucose-6-phosphate; F6P, fructose-6-phosphate; F16BP, fructose-1,6-biphosphate; GA3P, glyceraldehyde-3-phosphate; 13BPG, 1,3-biphosphate glycerate; PEP, phosphoenolpyruvate; Gr3P, glycerol-3-phosphate; Tgl, triglycerides; ACoA, acetyl-CoA; Cit, citrate; AKG, -ketogluterate; SCoA, succinyl-CoA; Suc, succinate; Mal, malate; Oxa, oxaloacetate; CoA, coenzyme-A (free); PCr, phosphocreatine; Cr, creatine; FADH2, reduced flavin adenine dinucleotide; FAD, oxidized flavin adenine dinucleotide; CK, creatine kinase; AK, adenylate kinase; HK, hexokinase; PFK, phosphofructokinase; LDH, lactate dedrogenase; PDH, pyruvate dehydrogenase. ETC+OxPhos, electron transport chain plus oxidative phosphorylation. </span> | ||
| + | |||
| + | |||
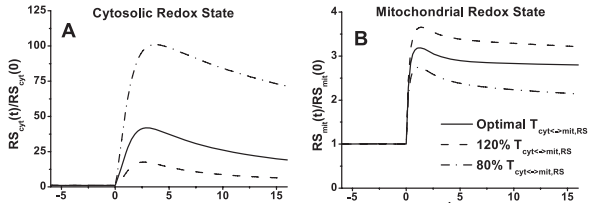
| + | <p align=justify>The model simulations of exercise response are consistent with the hypothesis that the cytosolic redox state is much more sensitive to the changes in mitochondrial NADH/NAD<sup>+</sup> shuttling activity and intracellular glycogen stores than the mitochondrial redox state. The dependence on NADH/NAD<sup>+</sup> shuttling activity between cytosol and mitochondria is simulated by changing the apparent transport rate coefficient T<sub>cyt<->mit,RS</sub> at the onset of exercise (Figure 10). Furthermore, muscle lactate production is regulated primarily by the cytosolic redox state. </p> | ||
| + | |||
| + | [[File:Li_etal_2009_fig10_model_predictions.png|center]] | ||
| + | |||
| + | <span style="font-size: 90%"> '''Figure 10 from (Li et al., 2009)''' <cite>26</cite>. Model-predicted dynamic responses of cytosolic redox state (NADH<sub>cyt</sub>/NAD<sup>+</sup><sub>cyt</sub>, RS<sub>cyt</sub>) (A), mitochondrial redox state (NADH<sub>mit</sub>/NAD<sup>+</sup><sub>mit</sub>, RS<sub>mit</sub>) (B) to moderate intensity exercise (60% VO<sub>2 max</sub>) and to variations in mitochondrial NADH/NAD<sup>+</sup> transporter (shuttling) activity parameter (T<sub>cyt<->mit,RS</sub>). The responses were computed using the optimal parameter estimates. Experimental data for these key state variables were not available in the literature for comparison. These state variables were normalized with respect to their resting values: [RS]<sub>cyt,0</sub> = [NADH]<sub>cyt,0</sub>/[NAD<sup>+</sup>]<sub>cyt,0</sub> = 0.00185 (A), [RS]<sub>mit,0</sub> = [NADH]<sub>mit,0</sub>/[NAD<sup>+</sup>]<sub>mit,0</sub> = 0.159 (B).</span> | ||
| + | |||
| + | |||
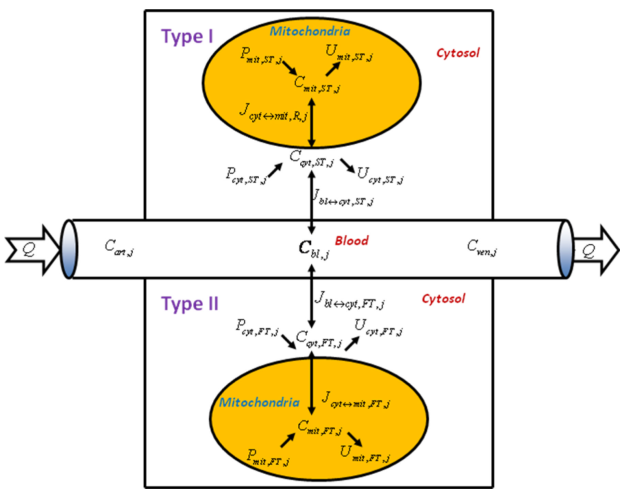
| + | <p align=justify> It is also noteworthy that the skeletal muscle is a heterogeneous tissue with different fiber types (Zierath and Hawley, 2004) <cite>27</cite>. Metabolic responses of the muscle fibers during exercise can reveal regulatory mechanisms that govern metabolism in skeletal muscle in health and disease states. Experimental measurements do not provide enough information to distinguish the extent of involvement of fiber type I and II during exercise. Although metabolite concentration changes cannot be directly related to the number of recruited fiber, they provide qualitative information of the fiber types involvement. Therefore, a quantitative characterization of the fiber activation includes not only the determination of metabolite and enzyme changes, but also a measure of the number of recruited fibers (i.e. type I and II). In order to tackle the problem Cabrera's group developed computational model (Li et al., 2012) <cite>4</cite> incorporating type I and II muscle fibers (Figure 11) which is based on a previous model that lacks this information (Li et al., 2009) <cite>26</cite>. An underlying hypothesis is that the recruitment and metabolic activation of the two main types of muscle fibers differ depending on the preexercise state and exercise protocols. An activation measured by metabolic response in single fibers is considered distinct from fiber recruitment characterized by the number (or mass) of each fiber type involved during a specific exercise. Each of the two parallel fiber compartments of the model, which share the same blood supply, is divided into cytosolic | ||
| + | and mitochondrial domains (Figure 11). Mass transport and reaction fluxes of key chemical species are distinguished in each fiber type. To simulate the skeletal muscle fibers metabolic response to moderate intensity exercise protocols using bicycle and knee extension, the model incorporates time-dependent rate coefficients that allow for changes in effective volumes and metabolic rates of each fiber. The metabolic and transport fluxes respond to exercise by a parallel activation mechanism (Li et al., 2009) <cite>26</cite>.</p> | ||
| + | |||
| + | [[File:Li_etal_2012_fig11_model_scheme.png|center]] | ||
| + | |||
| + | <span style="font-size: 90%"> '''Figure 11 from (Li et al., 2012)''' <cite>4</cite>. Schematic diagram of model structure. Whole skeletal muscle is composed of one blood domain and two tissue domains, corresponding to each muscle fiber, respectively. The fluid volume consists of capillary blood and interstitial fluid (ISF). Both muscle fiber types share a common blood supply. Each muscle fiber is compartmentalized as cytosol and mitochondria. Transport fluxes exist between blood and cytosol, and between cytosol and mitochondria. The species concentrations in tissue depend on reaction and transport fluxes.</span> | ||
| + | |||
| + | |||
| + | <p align=justify> Analysis of the model suggested that metabolic activation and recruitment of muscle fibers are closely related, but the degree of metabolic activation inferred from metabolite changes may differ from that of the fiber recruitment. Simulations with a mechanistic, mathematical model demonstrated that the activation as measured by metabolic response in single fibers is distinct from fiber recruitment that is characterized by the number (or mass) of each fiber type involved during a specific exercise. The results from this study underline the need for critical experiments that measure fiber recruitment and metabolism in order to simulate and quantify the contributions of type I and II fibers to the regulation of energy metabolism. Such experimental techniques could be used in combination with the computational model to investigate the relationships between the extents of metabolic activation, number of fibers recruited, and muscle groups engaged at different intensity exercise.</p> | ||
| + | |||
| + | ===Biomodels=== | ||
| + | <p align=justify>The search in [https://www.ebi.ac.uk/biomodels-main/ BioModels database] using query "skeletal muscle" returns 13 models (2 curated and 11 non-curated models), but not all of them can be considered as relevant for discussed tasks, while some of them have been already described above <cite>14</cite>; <cite>15</cite>. We distinguish these models on two classes: irrelevant and relevant (Table 1): </p> | ||
| + | |||
| + | {| class="wikitable" | ||
| + | ! Biomodels ID | ||
| + | ! Name | ||
| + | ! Short description | ||
| + | ! Reference | ||
| + | ! Relevance | ||
| + | |- | ||
| + | | '''''Curated models''''' | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |- | ||
| + | | <p align=justify><span style="font-size: 90%"> [https://www.ebi.ac.uk/biomodels-main/BIOMD0000000248 BIOMD0000000248]</span></p> | ||
| + | | <p align=justify><span style="font-size: 90%"> Lai2007_O2_Transport_Metabolism.</span></p> | ||
| + | | <p align=justify><span style="font-size: 90%"> The mathematical model simulates oxygen transport and metabolism in skeletal muscle in response to a step change from a warm-up steady state to a higher work rate corresponding to exercise at different levels of intensity: moderate (M), heavy (H) and very heavy (VH). </span></p> | ||
| + | | <p align=justify><span style="font-size: 90%"> Lai et al., 2007 <cite>28</cite> </span></p> | ||
| + | | <p align=justify><span style="font-size: 90%"> '''Relevant'''</span></p> | ||
| + | |- | ||
| + | | <p align=justify><span style="font-size: 90%"> [https://www.ebi.ac.uk/biomodels-main/BIOMD0000000574 BIOMD0000000574]</span></p> | ||
| + | | <p align=justify><span style="font-size: 90%"> Lai2014 - Hemiconcerted MWC model of intact calmodulin with two targets.</span></p> | ||
| + | | <p align=justify><span style="font-size: 90%"> Calmodulin is a calcium-binding protein ubiquitous in eukaryotic cells, involved in numerous calcium-regulated biological phenomena, such as synaptic plasticity, muscle contraction, cell cycle, and circadian rhythms. Authors built a mechanistic allosteric model of calmodulin, based on an hemiconcerted framework: each calmodulin lobe can exist in two conformations in thermodynamic equilibrium, with different affinities for calcium and different affinities for each target. Each lobe was allowed to switch conformation on its own. The model was parameterised and validated against experimental data from the literature. In spite of its simplicity, a two-state allosteric model was able to satisfactorily represent several sets of experiments, in particular the binding of calcium on intact and truncated calmodulin and the effect of different skMLCK peptides on calmodulin's saturation curve. The model can also be readily extended to include multiple targets.</span></p> | ||
| + | | <p align=justify><span style="font-size: 90%"> Lai et al., 2015 <cite>29</cite> </span></p> | ||
| + | | <p align=justify><span style="font-size: 90%"> '''Irrelevant'''</span></p> | ||
| + | |- | ||
| + | | '''''Non-curated models''''' | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |- | ||
| + | | <p align=justify><span style="font-size: 90%"> [https://www.ebi.ac.uk/biomodels-main/MODEL0912160004 MODEL0912160004]</span></p> | ||
| + | | <p align=justify><span style="font-size: 90%"> Shorten2007_SkeletalMuscleFatigue.</span></p> | ||
| + | | <p align=justify><span style="font-size: 90%"> Authors constructed a mathematical model of the skeletal muscle excitation-contraction pathway based on the cellular biochemical events that link excitation to contraction. The model includes descriptions of membrane voltage, calcium cycling and crossbridge dynamics and was parameterised and validated using the response characteristics of mouse skeletal muscle to a range of electrical stimuli. This model was used to uncover the complexities of skeletal muscle fatigue. We also parameterised our model to describe force kinetics in fast and slow twitch fibre types, which have a number of biochemical and biophysical differences. </span></p> | ||
| + | | <p align=justify><span style="font-size: 90%"> Shorten et al., 2007 <cite>30</cite> </span></p> | ||
| + | | <p align=justify><span style="font-size: 90%"> '''Relevant'''</span></p> | ||
| + | |- | ||
| + | | <p align=justify><span style="font-size: 90%"> [https://www.ebi.ac.uk/biomodels-main/MODEL1006230034 MODEL1006230034]</span></p> | ||
| + | | <p align=justify><span style="font-size: 90%"> Wu2006_ATPsynthesis_SkeletalMuscle.</span></p> | ||
| + | | <p align=justify><span style="font-size: 90%"> Authors used previously developed model of mitochondrial oxidative phosphorylation (Beard, 2005) <cite>17</cite> and data from <sup>31</sup>P-nuclear magnetic resonance spectroscopy of human forearm flexor muscle (Jeneson et al., 1993) <cite>18</cite> to test the hypothesis that substrate level (concentrations of ADP and inorganic phosphate) represents the primary signal governing the rate of mitochondrial ATP synthesis and maintaining the cellular ATP hydrolysis potential in skeletal muscle. Model-based predictions of cytoplasmic concentrations of phosphate metabolites (ATP, ADP, and Pi) matched data obtained from 20 healthy volunteers and indicated that as work rate is varied from rest to submaximal exercise commensurate increases in the rate of mitochondrial ATP synthesis are effected by changes in concentrations of available ADP and Pi. </span></p> | ||
| + | | <p align=justify><span style="font-size: 90%"> Wu et al., 2007 <cite>15</cite> </span></p> | ||
| + | | <p align=justify><span style="font-size: 90%"> '''Relevant'''</span></p> | ||
| + | |- | ||
| + | | <p align=justify><span style="font-size: 90%"> [https://www.ebi.ac.uk/biomodels-main/MODEL1006230049 MODEL1006230049]; [https://www.ebi.ac.uk/biomodels-main/MODEL1006230053 MODEL1006230053]; [https://www.ebi.ac.uk/biomodels-main/MODEL1006230077 MODEL1006230077]</span></p> | ||
| + | | <p align=justify><span style="font-size: 90%"> Vinnakota2006_MuscleGlycogenolysis_ModelC;_ModelB_ModelA.</span></p> | ||
| + | | <p align=justify><span style="font-size: 90%"> Authors <cite>14</cite> developed the model, which is aimed to explain the influence of pH on biochemical reaction kinetics (Figure 4) and equilibria by prediction of experimental data from the study of Scopes <cite>16</cite> on ''in vitro'' glycogenolysis using a cell free reconstituted enzyme system. They found that a wide range of experimental data, 13 time series out of 15 from three experiments, are explained by adjustment of only three kinetic parameters out of nearly 100 parameters, which leads to a significant conclusion that accurate accounting for the physical chemistry (pH-dependent enzyme kinetics) leads to a model with greater predictive power. </span></p> | ||
| + | | <p align=justify><span style="font-size: 90%"> Vinnakota et al., 2006 <cite>14</cite> </span></p> | ||
| + | | <p align=justify><span style="font-size: 90%"> '''Relevant'''</span></p> | ||
| + | |- | ||
| + | | <p align=justify><span style="font-size: 90%"> [https://www.ebi.ac.uk/biomodels-main/MODEL1006230090 MODEL1006230090]</span></p> | ||
| + | | <p align=justify><span style="font-size: 90%"> Wu2007_MitochondrialTCAcycle.</span></p> | ||
| + | | <p align=justify><span style="font-size: 90%"> A computational model of mitochondrial metabolism and electrophysiology is introduced and applied to analysis of data from isolated cardiac mitochondria and data on phosphate metabolites in striated muscle in vivo. This model is constructed based on detailed kinetics and thermodynamically balanced reaction mechanisms and a strict accounting of rapidly equilibrating biochemical species. Since building such a model requires introducing a large number of adjustable kinetic parameters, a correspondingly large amount of independent data from isolated mitochondria respiring on different substrates and subject to a variety of protocols is used to parameterize the model and ensure that it is challenged by a wide range of data corresponding to diverse conditions. The developed model is further validated by both in vitro data on isolated cardiac mitochondria and in vivo experimental measurements on human skeletal muscle. The validated model is used to predict the roles of NAD and ADP in regulating the tricarboxylic acid cycle dehydrogenase fluxes, demonstrating that NAD is the more important regulator. Further model predictions reveal that a decrease of cytosolic pH value results in decreases in mitochondrial membrane potential and a corresponding drop in the ability of the mitochondria to synthesize ATP at the hydrolysis potential required for cellular function. </span></p> | ||
| + | | <p align=justify><span style="font-size: 90%"> Wu et al., 2007 <cite>31</cite> </span></p> | ||
| + | | <p align=justify><span style="font-size: 90%"> '''Relevant'''</span></p> | ||
| + | |- | ||
| + | | <p align=justify><span style="font-size: 90%"> [https://www.ebi.ac.uk/biomodels-main/MODEL1012220002 MODEL1012220002]</span></p> | ||
| + | | <p align=justify><span style="font-size: 90%"> Caron2010_mTOR_SignalingNetwork.</span></p> | ||
| + | | <p align=justify><span style="font-size: 90%"> The mammalian target of rapamycin (mTOR) is a central regulator of cell growth and proliferation. Using CellDesigner, a modeling support software for graphical notation, authors presented herein a comprehensive map of the mTOR signaling network, which includes 964 species connected by 777 reactions. The map complies with both the systems biology markup language (SBML) and graphical notation (SBGN) for computational analysis and graphical representation, respectively. This comprehensive map of the mTOR network will serve as a tool to facilitate systems‐level study of up‐to‐date mTOR network components and signaling events toward the discovery of novel regulatory processes. </span></p> | ||
| + | | <p align=justify><span style="font-size: 90%"> Caron et al., 2010 <cite>32</cite> </span></p> | ||
| + | | <p align=justify><span style="font-size: 90%"> '''Relevant'''</span></p> | ||
| + | |- | ||
| + | | <p align=justify><span style="font-size: 90%"> [https://www.ebi.ac.uk/biomodels-main/MODEL1172940336 MODEL1172940336]</span></p> | ||
| + | | <p align=justify><span style="font-size: 90%"> DePaor1986_CirculatoryAutoregulation.</span></p> | ||
| + | | <p align=justify><span style="font-size: 90%"> Circulatory autregulation is the phenomenon whereby an isolated organ can maintain a constant or almost-constant blood flow rate over a range of perfusion pressures. A mathematical model is developed, based on work reported in the physiological literature, and tuned to show that autoregulation can be accomplished by pressure-induced oscillations in arteriolar radius. Various features known lo be exhibited by skeletal muscle and by stretch receptors are incorporated in the model of smooth muscle surrounding the arterioles. </span></p> | ||
| + | | <p align=justify><span style="font-size: 90%"> De Paor and Timmons, 1986 <cite>33</cite> </span></p> | ||
| + | | <p align=justify><span style="font-size: 90%"> '''Irrelevant'''</span></p> | ||
| + | |- | ||
| + | | <p align=justify><span style="font-size: 90%"> [https://www.ebi.ac.uk/biomodels-main/MODEL1310110011 MODEL1310110011]</span></p> | ||
| + | | <p align=justify><span style="font-size: 90%"> Thiele2013 - Skeletal muscle myocytes.</span></p> | ||
| + | | <p align=justify><span style="font-size: 90%"> The model of skeletal muscle myocytes metabolism is derived from the community-driven global reconstruction of human metabolism (version 2.02, [http://identifiers.org/biomodels.db/MODEL1109130000 MODEL1109130000]). </span></p> | ||
| + | | <p align=justify><span style="font-size: 90%"> Thiele et al., 2013 <cite>34</cite> </span></p> | ||
| + | | <p align=justify><span style="font-size: 90%"> '''Irrelevant'''</span></p> | ||
| + | |- | ||
| + | | <p align=justify><span style="font-size: 90%"> [https://www.ebi.ac.uk/biomodels-main/MODEL1603150001 MODEL1603150001]</span></p> | ||
| + | | <p align=justify><span style="font-size: 90%"> Swainston2016 - Reconstruction of human metabolic network (Recon 2.2).</span></p> | ||
| + | | <p align=justify><span style="font-size: 90%"> Authors developed Recon 2.2, the most predictive model of human metabolism to date as demonstrated here. Extensive manual curation has increased the reconstruction size to 5324 metabolites, 7785 reactions and 1675 associated genes, which now are mapped to a single standard. The focus upon mass and charge balancing of all reactions, along with better representation of energy generation, has produced a flux model that correctly predicts ATP yield on different carbon sources. </span></p> | ||
| + | | <p align=justify><span style="font-size: 90%"> Swainston et al., 2016 <cite>35</cite> </span></p> | ||
| + | | <p align=justify><span style="font-size: 90%"> '''Irrelevant'''</span></p> | ||
| + | |- | ||
| + | | <p align=justify><span style="font-size: 90%"> [https://www.ebi.ac.uk/biomodels-main/MODEL6399676120 MODEL6399676120]</span></p> | ||
| + | | <p align=justify><span style="font-size: 90%"> Duarte2007_Homo_sapiens_Metabol_Recon_1.</span></p> | ||
| + | | <p align=justify><span style="font-size: 90%"> Authors manually reconstructed the global human metabolic network based on Build 35 of the genome annotation and a comprehensive evaluation of >50 years of legacy data (i.e., bibliomic data). Herein they describe the reconstruction process and demonstrate how the resulting genome-scale (or global) network can be used (i) for the discovery of missing information, (ii) for the formulation of an in silico model, and (iii) as a structured context for analyzing high-throughput biological data sets. </span></p> | ||
| + | | <p align=justify><span style="font-size: 90%"> Duarte et al., 2007 <cite>36</cite> </span></p> | ||
| + | | <p align=justify><span style="font-size: 90%"> '''Irrelevant'''</span></p> | ||
| + | |} | ||
| + | |||
| + | <span style="font-size: 90%"> '''Table1'''. The result of search in BioModels database using query "''skeletal muscle''".</span> | ||
| + | |||
| + | |||
| + | ===Conclusion=== | ||
| + | <p align=justify> The model approaches discussed above address various spatial, temporal and biochemical resolutions and are conceptually complementary. However, they were not yet linked in an integrated computational framework and executed simultaneously using a modular approach (Snoep et al., 2006) <cite>37</cite> that has been implemented in [http://wiki.biouml.org/index.php/BioUML_wiki BioUML platform]. Computational modeling of metabolic responses of skeletal muscle to physiological stresses (e.g., hypoxia, ischemia, and exercise) is intended to quantitatively elucidate regulatory mechanisms. Although more detailed mechanisms can be included, these cannot be effectively validated without appropriate ''in vivo'' experimental data. With the availability of additional data, the model could incorporate and test alternative mechanisms of the regulation. The fact that available models do not account for blood flow heterogeneity and all fiber type distributions associated with skeletal muscle cellular metabolism constrains the application of virtual physiological modelling to sports or space travel.But the most significant limitation of the present models is that they do not account for detailed interconnetction between signaling pathways activated by physiological stresses and downstream changes on coupled transcriptional and metabolic levels using positive and negative feedbacks. In order to overcome these shortcomings, we are going to extend previously developed model (Li et al., 2009) <cite>26</cite> incorporating essential steps of [http://virtualbiology.biouml.org/index.php/AMPK AMPK signaling pathway] in skeletal muscle which is regulated in a distinct manner during contraction depending on exercise intensity and duration.</p> | ||
| − | |||
===References=== | ===References=== | ||
| Line 103: | Line 230: | ||
#25 pmid=18390321 <!-- Dash et al 2008 --> | #25 pmid=18390321 <!-- Dash et al 2008 --> | ||
#26 pmid=18829894 <!-- Li et al 2009 --> | #26 pmid=18829894 <!-- Li et al 2009 --> | ||
| + | #27 pmid=15486583 <!-- Zierath and Hawley 2004 --> | ||
| + | #28 pmid=17380394 <!-- Lai et al 2007 --> | ||
| + | #29 pmid=25611683 <!-- Lai et al 2014 --> | ||
| + | #30 pmid=18080210 <!-- Shorten et al 2007 --> | ||
| + | #31 pmid=17591785 <!-- Wu et al 2007 --> | ||
| + | #32 pmid=21179025 <!-- Caron et al 2010 --> | ||
| + | #33 https://www.tandfonline.com/doi/abs/10.1080/00207178608933494 <!-- De Paor and Timmons 1986 --> | ||
| + | #34 pmid=23455439 <!-- Thiele et al 2013 --> | ||
| + | #35 https://link.springer.com/article/10.1007%2Fs11306-016-1051-4 <!-- Swainston et al 2016 --> | ||
| + | #36 pmid=17267599 <!-- Duarte et al 2007 --> | ||
| + | #37 pmid=16242236 <!-- Snoep et al 2006 --> | ||
</biblio> | </biblio> | ||
| + | |||
| + | [[Category: Human_muscle]] | ||
| + | [[Category: Model]] | ||
| + | [[Category: Exercise]] | ||
Latest revision as of 16:50, 28 May 2021
Contents
Introduction
Skeletal muscle is one of the most abundant tissues in mammals, accounting for up to 40% of the total mass ofthe human body (Janssen et al., 2000) [1]. The contraction–relaxation cycle in muscle requires energy that is mostly generated aerobically by mitochondria particularly abundant in adult muscle fibres. It is worth to note that skeletal muscle can maintain ATP concentration constant during the transition from rest to exercise, whereas metabolic reaction rates may increase substantially (Kunz, 2001) [2]. Although it is well known that skeletal muscle adaptations to exercise depend on duration, intensity, and frequency, changes in muscle proteins associated with different types of exercise have not been well characterized (Gonzalez‐Freire et al., 2017) [3]. Moreover, the quantitative contributions of different fiber types to the energy demand and detailed dynamics of metabolic responses of the skeletal muscle in response to different exercise intensities are unknown. Indeed, accurate measurements to quantify the recruitment and metabolic activation of muscle fibers in vivo have not been possible to date (Li et al., 2012) [4]. So due to a shortage of dynamic in vivo human data, the regulatory mechanisms of functioning of the skeletal muscle metabolism are poorly understood. To quantitatively interpret the limited data, a physiologically based mathematical modeling approach can be applied (Li et al., 2010) [5].
Published models
Korzeniewski models
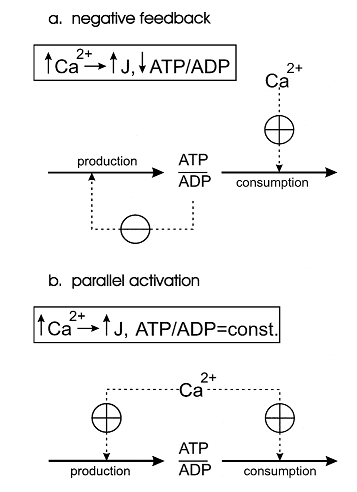
One of the first theoretical investigation in this field was conducted by Bernard Korzeniewski (Korzeniewski, 1998,1999) [6][7]. He developed the computational model of oxidative phosphorylation (OxP) in skeletal muscle mitochondria in order to decipher a regulatory mechanism of the adjustment of ATP production to ATP consumption in contracting muscle. During the transition from the resting state of muscles to their maximal exercise, there is a great increase in energy demand (ATP consumption). Mitochondrial OxP is the main process responsible for ATP production in most muscle fibre types under most conditions. Therefore, mitochondria have to ‘know’ in some way how fast should they produce ATP in a given moment of time to meet the rate of energy consumption and to avoid a drastic decrease in cytosolic phosphorylation potential which would hinder muscle contraction.Two alternative mechanisms of the adjusting the energy (ATP) production rate to the energy consumption rate were postulated. They can be called the ‘negative feedback’ and ‘parallel activation’ (Figure 1).
Figure 1 from (Korzeniewski, 1998) [6]. Comparison of the negative feedback and parallel activation mechanisms. (a) Negative feedback; only ATP consumption is activated directly by an external effector (for example calcium ions), while ATP production is activated indirectly, via a significant decrease in the ATP/ADP ratio. (b) Parallel activation ; both ATP consumption and ATP production are directly activated by an external effector; the ATP/ADP ratio remains approximately constant.
The model of OxP in skeletal muscle mitochondria showed that the only quantitatively valid explanation of the existing experimental data is that the parallel activation of different steps constitutes the main mechanism responsible for the adjustment of the ATP production rate to the current energy demand in working muscle and that the intuitive interpretations based on the negative feedback mechanism, although qualitatively logical, do not work when quantitative changes in fluxes and metabolite concentrations as well as the kinetic properties of mitochondria are taken into account.
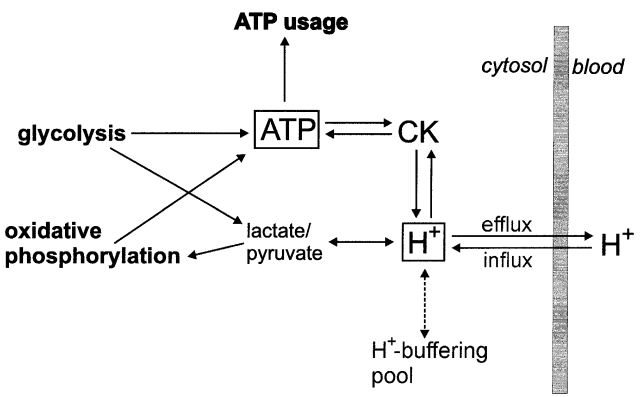
At the next step the comprehensive model of glycolysis in skeletal muscle developed by Lambeth and Kushmerick (Lambeth and Kushmerick, 2002)[8], describing the glycolytic flux as a function of [ADP], [AMP], [ATP] and [Pi], was incorporated to the model of OxP in intact skeletal muscle (Korzeniewski and Liguzinski, 2004)[9].
Figure 2 from (Korzeniewski and Liguzinski, 2004) [9]. Scheme of processes producing, consuming and buffering cytosolic ATP and H+ in skeletal muscle.
Computer simulations presented in the study were performed either using the model of OxP plus comprehensive model of glycolysis (these mode of simulations was called Mode 0) or the model of OxP containing the simple kinetic description of the glycolytic flux as a function of ADP concentration. In the latter case, three further modes of simulations were used:
1) in Mode 1, no ATP and H+ production by anaerobic glycolysis is involved (it is assumed that the pyruvate/lactate/proton production by glycolysis is always equal to the pyruvate/lactate/proton consumption by OxP);
2) in Mode 2, only the dependence of the glycolytic flux on ADP and the direct activation of glycolysis during muscle contraction are included;
3) in Mode 3, the glycolytic flux is described as depending on both ADP and H+, and is also directly activated during muscle contraction. Thus, the production of ATP and H+ by anaerobic glycolysis is allowed in Mode 2 and Mode 3.
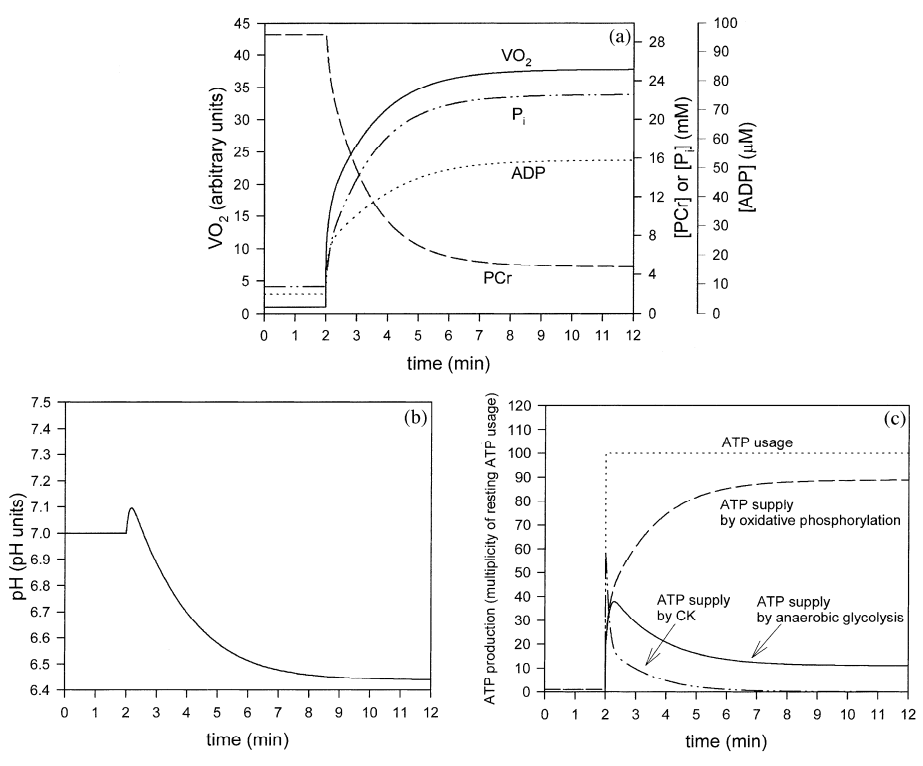
Generally, it can be concluded that Mode 3 (dependence of glycolysis on ADP and H+) gives predictions much better matching experimental results than the predictions produced within Mode 2 (dependence of glycolysis on ADP only). Namely, the simulations in Mode 3 predict the transient activation of anaerobic glycolysis and the proper extent and duration of the initial alkalization. Therefore, it can be concluded that the regulation of glycolysis in muscle during transition from rest to work is a result of the dynamic balance between the activation of this metabolic pathway by ADP, AMP, Pi and alkalization, direct activation by some cytosolic factor during muscle contraction and the inhibition of glycolysis by acidification.
Figure 3 from (Korzeniewski and Liguzinski, 2004) [9]. Simulated behavior of the bioenergetic system in muscle in Mode 3 during transition from rest to intensive exercise. Mode 3: direct activation of glycolysis during muscle contraction, activation of glycolysis by ADP (plus AMP and Pi), inhibition of glycolysis by H+. After first 2 min of simulation, representing resting steady-state, ATP usage was increased 100 times. In the same moment, glycolysis was directly activated 1000.8 times and OxP was activated 1000.4 times. (a) time courses of VO2 (standardized for 1 in resting state), ADP, PCr and Pi; (b) time course of cytosolic pH; (c) time courses of ATP usage, ATP supply by creatine kinase, ATP supply by anaerobic glycolysis and ATP supply by OxP (including aerobic glycolysis).
OxP+glycolysis models
It must be emphasized that the computer model of OxP+glycolysis used in the present study contains several simplifications and approximations. First, a simple linear dependence of the glycolytic flux on [ADP] was extracted from the initial model (Lambeth and Kushmerick, 2002)[8]. This was justified by the fact that the regulation by ADP, AMP and Pi cannot alone account for the kinetic properties of glycolysis in intact muscle. Such a simple description allowed including in the model the direct activation of glycolysis by some contraction-related factor and the inhibition of this process by protons. Second, a simple linear dependence of the glycolytic flux on [H+] was assumed. However, the real dependence may be more complicated. This may be the reason why the simulated initial transient activation of anaerobic glycolysis lasts a little longer than in reality, and, consequently, causes a longer transition of VO2 to the active steady-state than that observed in experimental studies (Ceretelli et al., 1979) [10]; (Hughson et al., 2001) [11]. Third, a simplified kinetic description of the direct activation of glycolysis (n^x) was used. Fourth, the slow component in the oxygen uptake kinetics, observed in the intact muscle above the lactate threshold (Whipp and Wasserman, 1972) [12], is not taken into account within the model. Fifth, it is assumed that OxP is directly activated by some external cytosolic factor (e.g. calcium ions) instantly after an onset of exercise. This is the reason of the very quick initial increase in the respiration rate. However, this is most probably only a rough approximation of the real situation, because calcium needs some time to enter mitochondria and to activate mitochondrial enzymes. Thus, this model can be improved and extended in many aspects and directions. First, a complete, detailed kinetic description of the tricarboxylate acid cycle (TCA), glycolysis and fatty acid hoxidation can be incorporated into this model. Second, the model can be extended in order to simulate the behavior of the system during extremely intensive short-term exercise, where anaerobic glycolysis is the predominant source of ATP (Korzeniewski and Liguzinski, 2004) [9].
A set of integrated computational model describing different cellular factors (concentration of free ADP, Pi or pH level in the cell) regulating OxP and glycolysis has been developed (Mader, 2003) [13]; (Vinnakota et al., 2006) [14]; (Wu et al., 2007) [15]. Namely, Mader [13] presented a mathematical description of the regulation of ATP production (or the activity of OxP) in muscle cells as a function of (1) free [ADP] as the substrate and (2) a second driving force F*deltaG (kilojoules per mole) resulting from the difference of free energy deltaG_ox,ap (kilojoules per mole) – deltaG_ATP,cyt (kilojoules per mole), which is necessary to sustain the flow of ATP from inside the mitochondrian to the cytosol. Results from the computational simulations demonstrated a high level of similarity with the experimentally observed dynamic behaviour of measurable parameters of OxP, glycolysis and the behaviour of the parameters of the cytosolic high energy phosphate system. Furthermore, the computational simulations showed that complex dynamic behaviour in real biological systems can be ruled by a few general principles and a relatively simple set of equations. It is, however, emphasized by author that the model needs a more detailed implementation of the characteristics of the reactions occurring at the site of the mitochondria. In turn, Vinnakota with co-authors [14] developed the model, which is aimed to explain the influence of pH on biochemical reaction kinetics (Figure 4) and equilibria by prediction of experimental data from the study of Scopes [16] on in vitro glycogenolysis using a cell free reconstituted enzyme system (Figure 5). They found that a wide range of experimental data, 13 time series out of 15 from three experiments, are explained by adjustment of only three kinetic parameters out of nearly 100 parameters, which leads to a significant conclusion that accurate accounting for the physical chemistry (pH-dependent enzyme kinetics) leads to a model with greater predictive power.
|
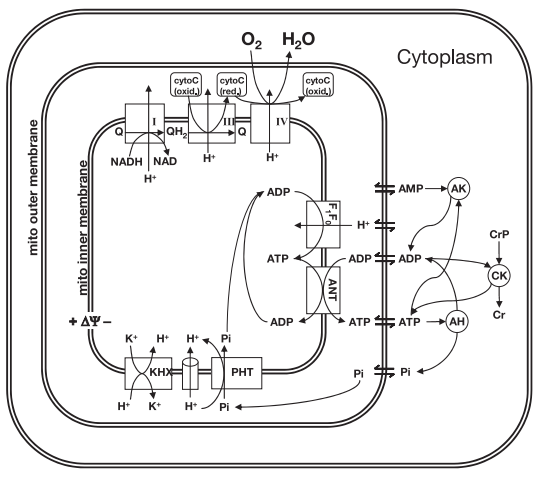
Wu and co-authors [15] used previously developed model (Figure 6) of mitochondrial oxidative phosphorylation (Beard, 2005) [17] and data from 31P-nuclear magnetic resonance spectroscopy of human forearm flexor muscle (Jeneson et al., 1993) [18] to test the hypothesis that substrate level (concentrations of ADP and inorganic phosphate) represents the primary signal governing the rate of mitochondrial ATP synthesis and maintaining the cellular ATP hydrolysis potential in skeletal muscle.
Figure 6 from (Wu et al., 2007) [15]. Illustration of components included in the computational model of oxidative phosphorylation in skeletal muscular cells. All reactions and mass transport take place in three compartments: cytoplasm, mitochondrial intermembrane space, and mitochondrial matrix. ANT, adenine nucleotide translocase; ΔΨ, mitochondrial membrane potential; CK, creatine (Cr) kinase; AK, adenylate kinase; AH, (please define).
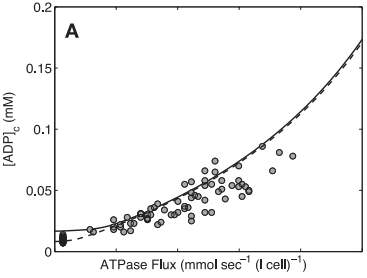
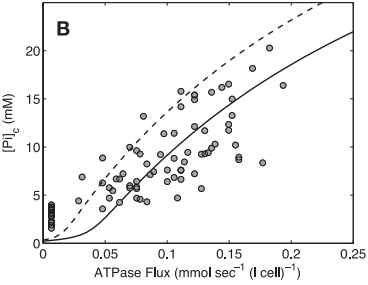
Model-based predictions of cytoplasmic concentrations of phosphate metabolites (ATP, ADP, and Pi) matched data obtained from 20 healthy volunteers and indicated that as work rate is varied from rest to submaximal exercise commensurate increases in the rate of mitochondrial ATP synthesis are effected by changes in concentrations of available ADP and Pi (Figure 7).
Figure 7 from (Wu et al., 2007) [15]. Model prediction of ADP concentration and inorganic phosphate concentration in cytoplasm as a function of ATP hydrolysis rate in the healthy subjects. A: plot of predicted ADP concentration in cytoplasm, [ADP]c, as a function of ATP hydrolysis rate, ATPase flux. B: plot of predicted Pi concentration in cytoplasm, [Pi]c, as a function of ATP hydrolysis rate, ATPase flux. The solid and dashed lines represent model-predicted results. The circles represent experimentally measured estimation from Jeneson et al. [18]. Solid line correspond to the optimal value of the total pool of exchangeable phosphate (TPP) = 36.8 mM; dashed lines correspond to TPP = 40.5 mM (10% greater than the optimal value).
Cabrera models
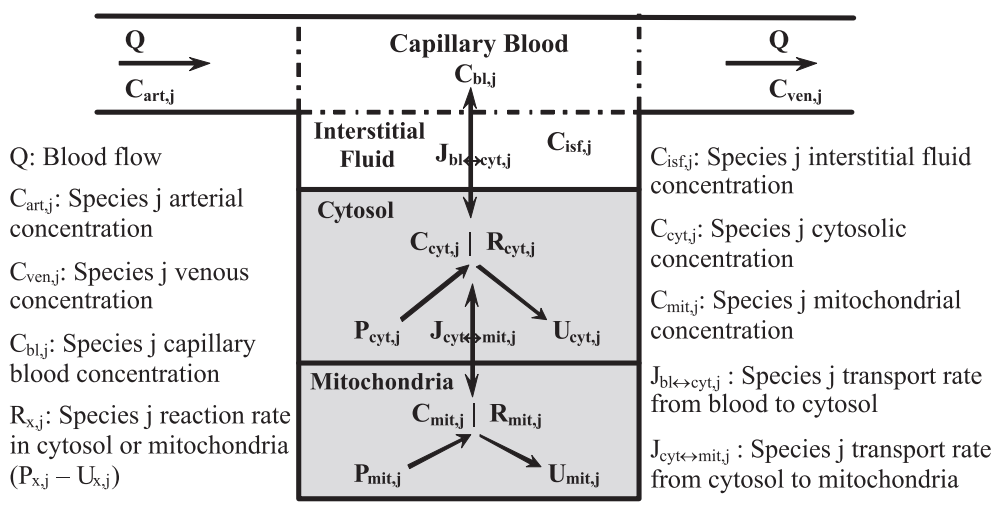
The mechanistic basis for addressing key questions with respect to the mechanisms of metabolic regulation in contracting skeletal muscle was provided by group of Prof. Marco Cabrera (Case Western Reserve University, Cleveland, Ohio) using a set of developed mathematical models [4]; [5]; [19]; [20]; [21]; [22]; [23]; [24]; [25]; [26]. In particularly, a physiologically based mathematical model of cellular metabolism in perfused skeletal muscle that simulates metabolic responses to moderate intensity exercise (60% VO2max) (Li et al., 2009) [26] differs significantly from their previous models of cardiac and skeletal muscle cellular metabolism and other published models of skeletal muscle cellular metabolism in that both the biochemical reactions governing cellular metabolism are considered reversible with their fluxes satisfying Haldane relationships (thermodynamic constraints) and the model incorporates the primary substrates (glucose and free fatty acids (FFAs)) together with key metabolic pathways of cellular metabolism (glycolysis, lipid metabolism, CK, TCA cycle, and oxidative phosphorylation). The model distinguishes metabolic processes occurring in capillary blood, cytosol, and mitochondria and incorporates distinct transport processes between these domains (Figures 8-9).
Figure 8 from (Li et al., 2009) [26]. Schematic diagram of the structure of the model for blood-tissue cell exchange and cellular metabolism in skeletal muscle. The compartments are assumed to be perfectly mixed, and the capillary blood and tissue interstitial fluid (ISF) domains are assumed to be in phase-equilibrium with each other so that Cisf, j = Cbl, j = Cven, j for any chemical species j. The tissue cells domain is further compartmentalized into the cytosolic and mitochondrial domains with the chemical species having distinct dynamics in these 2 subcellular domains. A total of 9 species [glucose (Glc), lactate (Lac), pyruvate (Pyr), alanine (Ala), free fatty acid (FFA), glycerol (Glr), CO2, O2, and H+ (protons)] undergo bloodcytosol exchange, and 11 species [Pyr, fatty acyl-CoA (FAC), CoA, reduced nicotinamide adenine dinucleotide (NADH), oxidized nicotinamide adenine dinucleotide (NAD+), ATP, ADP, inorganic phosphate (Pi), CO2, O2, and H+] undergo cytosol-mitochondria exchange.
This comprehensive computational model accounts for proton handling and considers the coupled energy controller pairs ATP-ADP and NADH-NAD+ as cosubstrates. A key feature of the model is its ability to simulate blood and tissue responses, which are routinely measured in experimental studies, as well as to predict dynamic intracellular species concentrations and reaction rates, which cannot be measured with the currently available experimental techniques. The underlying hypothesis of the model is that during the transition from rest to exercise, the cytosolic redox state is more sensitive to metabolic disturbance than the mitochondrial redox state. This hypothesis was tested by simulating skeletal muscle metabolic responses during moderate intensity exercise [60% maximal O2 consumption (VO2max)] with different transport (shuttling) rates of reducing equivalents (NADH and NAD+) between cytosol and mitochondria and different intracellular glycogen concentrations.
Figure 9 from (Li et al., 2009) [26]. Schematic diagram of biochemical pathways depicting various chemical reactions and species involved in the cellular metabolism of skeletal muscle. The reactions and species are further compartmentalized into the cytosolic and mitochondrial reactions and species. Gly, glycogen; G6P, glucose-6-phosphate; F6P, fructose-6-phosphate; F16BP, fructose-1,6-biphosphate; GA3P, glyceraldehyde-3-phosphate; 13BPG, 1,3-biphosphate glycerate; PEP, phosphoenolpyruvate; Gr3P, glycerol-3-phosphate; Tgl, triglycerides; ACoA, acetyl-CoA; Cit, citrate; AKG, -ketogluterate; SCoA, succinyl-CoA; Suc, succinate; Mal, malate; Oxa, oxaloacetate; CoA, coenzyme-A (free); PCr, phosphocreatine; Cr, creatine; FADH2, reduced flavin adenine dinucleotide; FAD, oxidized flavin adenine dinucleotide; CK, creatine kinase; AK, adenylate kinase; HK, hexokinase; PFK, phosphofructokinase; LDH, lactate dedrogenase; PDH, pyruvate dehydrogenase. ETC+OxPhos, electron transport chain plus oxidative phosphorylation.
The model simulations of exercise response are consistent with the hypothesis that the cytosolic redox state is much more sensitive to the changes in mitochondrial NADH/NAD+ shuttling activity and intracellular glycogen stores than the mitochondrial redox state. The dependence on NADH/NAD+ shuttling activity between cytosol and mitochondria is simulated by changing the apparent transport rate coefficient Tcyt<->mit,RS at the onset of exercise (Figure 10). Furthermore, muscle lactate production is regulated primarily by the cytosolic redox state.
Figure 10 from (Li et al., 2009) [26]. Model-predicted dynamic responses of cytosolic redox state (NADHcyt/NAD+cyt, RScyt) (A), mitochondrial redox state (NADHmit/NAD+mit, RSmit) (B) to moderate intensity exercise (60% VO2 max) and to variations in mitochondrial NADH/NAD+ transporter (shuttling) activity parameter (Tcyt<->mit,RS). The responses were computed using the optimal parameter estimates. Experimental data for these key state variables were not available in the literature for comparison. These state variables were normalized with respect to their resting values: [RS]cyt,0 = [NADH]cyt,0/[NAD+]cyt,0 = 0.00185 (A), [RS]mit,0 = [NADH]mit,0/[NAD+]mit,0 = 0.159 (B).
It is also noteworthy that the skeletal muscle is a heterogeneous tissue with different fiber types (Zierath and Hawley, 2004) [27]. Metabolic responses of the muscle fibers during exercise can reveal regulatory mechanisms that govern metabolism in skeletal muscle in health and disease states. Experimental measurements do not provide enough information to distinguish the extent of involvement of fiber type I and II during exercise. Although metabolite concentration changes cannot be directly related to the number of recruited fiber, they provide qualitative information of the fiber types involvement. Therefore, a quantitative characterization of the fiber activation includes not only the determination of metabolite and enzyme changes, but also a measure of the number of recruited fibers (i.e. type I and II). In order to tackle the problem Cabrera's group developed computational model (Li et al., 2012) [4] incorporating type I and II muscle fibers (Figure 11) which is based on a previous model that lacks this information (Li et al., 2009) [26]. An underlying hypothesis is that the recruitment and metabolic activation of the two main types of muscle fibers differ depending on the preexercise state and exercise protocols. An activation measured by metabolic response in single fibers is considered distinct from fiber recruitment characterized by the number (or mass) of each fiber type involved during a specific exercise. Each of the two parallel fiber compartments of the model, which share the same blood supply, is divided into cytosolic and mitochondrial domains (Figure 11). Mass transport and reaction fluxes of key chemical species are distinguished in each fiber type. To simulate the skeletal muscle fibers metabolic response to moderate intensity exercise protocols using bicycle and knee extension, the model incorporates time-dependent rate coefficients that allow for changes in effective volumes and metabolic rates of each fiber. The metabolic and transport fluxes respond to exercise by a parallel activation mechanism (Li et al., 2009) [26].
Figure 11 from (Li et al., 2012) [4]. Schematic diagram of model structure. Whole skeletal muscle is composed of one blood domain and two tissue domains, corresponding to each muscle fiber, respectively. The fluid volume consists of capillary blood and interstitial fluid (ISF). Both muscle fiber types share a common blood supply. Each muscle fiber is compartmentalized as cytosol and mitochondria. Transport fluxes exist between blood and cytosol, and between cytosol and mitochondria. The species concentrations in tissue depend on reaction and transport fluxes.
Analysis of the model suggested that metabolic activation and recruitment of muscle fibers are closely related, but the degree of metabolic activation inferred from metabolite changes may differ from that of the fiber recruitment. Simulations with a mechanistic, mathematical model demonstrated that the activation as measured by metabolic response in single fibers is distinct from fiber recruitment that is characterized by the number (or mass) of each fiber type involved during a specific exercise. The results from this study underline the need for critical experiments that measure fiber recruitment and metabolism in order to simulate and quantify the contributions of type I and II fibers to the regulation of energy metabolism. Such experimental techniques could be used in combination with the computational model to investigate the relationships between the extents of metabolic activation, number of fibers recruited, and muscle groups engaged at different intensity exercise.
Biomodels
The search in BioModels database using query "skeletal muscle" returns 13 models (2 curated and 11 non-curated models), but not all of them can be considered as relevant for discussed tasks, while some of them have been already described above [14]; [15]. We distinguish these models on two classes: irrelevant and relevant (Table 1):
| Biomodels ID | Name | Short description | Reference | Relevance |
|---|---|---|---|---|
| Curated models | ||||
| Lai2007_O2_Transport_Metabolism. |
The mathematical model simulates oxygen transport and metabolism in skeletal muscle in response to a step change from a warm-up steady state to a higher work rate corresponding to exercise at different levels of intensity: moderate (M), heavy (H) and very heavy (VH). |
Lai et al., 2007 [28] |
Relevant | |
| Lai2014 - Hemiconcerted MWC model of intact calmodulin with two targets. |
Calmodulin is a calcium-binding protein ubiquitous in eukaryotic cells, involved in numerous calcium-regulated biological phenomena, such as synaptic plasticity, muscle contraction, cell cycle, and circadian rhythms. Authors built a mechanistic allosteric model of calmodulin, based on an hemiconcerted framework: each calmodulin lobe can exist in two conformations in thermodynamic equilibrium, with different affinities for calcium and different affinities for each target. Each lobe was allowed to switch conformation on its own. The model was parameterised and validated against experimental data from the literature. In spite of its simplicity, a two-state allosteric model was able to satisfactorily represent several sets of experiments, in particular the binding of calcium on intact and truncated calmodulin and the effect of different skMLCK peptides on calmodulin's saturation curve. The model can also be readily extended to include multiple targets. |
Lai et al., 2015 [29] |
Irrelevant | |
| Non-curated models | ||||
| Shorten2007_SkeletalMuscleFatigue. |
Authors constructed a mathematical model of the skeletal muscle excitation-contraction pathway based on the cellular biochemical events that link excitation to contraction. The model includes descriptions of membrane voltage, calcium cycling and crossbridge dynamics and was parameterised and validated using the response characteristics of mouse skeletal muscle to a range of electrical stimuli. This model was used to uncover the complexities of skeletal muscle fatigue. We also parameterised our model to describe force kinetics in fast and slow twitch fibre types, which have a number of biochemical and biophysical differences. |
Shorten et al., 2007 [30] |
Relevant | |
| Wu2006_ATPsynthesis_SkeletalMuscle. |
Authors used previously developed model of mitochondrial oxidative phosphorylation (Beard, 2005) [17] and data from 31P-nuclear magnetic resonance spectroscopy of human forearm flexor muscle (Jeneson et al., 1993) [18] to test the hypothesis that substrate level (concentrations of ADP and inorganic phosphate) represents the primary signal governing the rate of mitochondrial ATP synthesis and maintaining the cellular ATP hydrolysis potential in skeletal muscle. Model-based predictions of cytoplasmic concentrations of phosphate metabolites (ATP, ADP, and Pi) matched data obtained from 20 healthy volunteers and indicated that as work rate is varied from rest to submaximal exercise commensurate increases in the rate of mitochondrial ATP synthesis are effected by changes in concentrations of available ADP and Pi. |
Wu et al., 2007 [15] |
Relevant | |
| Vinnakota2006_MuscleGlycogenolysis_ModelC;_ModelB_ModelA. |
Authors [14] developed the model, which is aimed to explain the influence of pH on biochemical reaction kinetics (Figure 4) and equilibria by prediction of experimental data from the study of Scopes [16] on in vitro glycogenolysis using a cell free reconstituted enzyme system. They found that a wide range of experimental data, 13 time series out of 15 from three experiments, are explained by adjustment of only three kinetic parameters out of nearly 100 parameters, which leads to a significant conclusion that accurate accounting for the physical chemistry (pH-dependent enzyme kinetics) leads to a model with greater predictive power. |
Vinnakota et al., 2006 [14] |
Relevant | |
| Wu2007_MitochondrialTCAcycle. |
A computational model of mitochondrial metabolism and electrophysiology is introduced and applied to analysis of data from isolated cardiac mitochondria and data on phosphate metabolites in striated muscle in vivo. This model is constructed based on detailed kinetics and thermodynamically balanced reaction mechanisms and a strict accounting of rapidly equilibrating biochemical species. Since building such a model requires introducing a large number of adjustable kinetic parameters, a correspondingly large amount of independent data from isolated mitochondria respiring on different substrates and subject to a variety of protocols is used to parameterize the model and ensure that it is challenged by a wide range of data corresponding to diverse conditions. The developed model is further validated by both in vitro data on isolated cardiac mitochondria and in vivo experimental measurements on human skeletal muscle. The validated model is used to predict the roles of NAD and ADP in regulating the tricarboxylic acid cycle dehydrogenase fluxes, demonstrating that NAD is the more important regulator. Further model predictions reveal that a decrease of cytosolic pH value results in decreases in mitochondrial membrane potential and a corresponding drop in the ability of the mitochondria to synthesize ATP at the hydrolysis potential required for cellular function. |
Wu et al., 2007 [31] |
Relevant | |
| Caron2010_mTOR_SignalingNetwork. |
The mammalian target of rapamycin (mTOR) is a central regulator of cell growth and proliferation. Using CellDesigner, a modeling support software for graphical notation, authors presented herein a comprehensive map of the mTOR signaling network, which includes 964 species connected by 777 reactions. The map complies with both the systems biology markup language (SBML) and graphical notation (SBGN) for computational analysis and graphical representation, respectively. This comprehensive map of the mTOR network will serve as a tool to facilitate systems‐level study of up‐to‐date mTOR network components and signaling events toward the discovery of novel regulatory processes. |
Caron et al., 2010 [32] |
Relevant | |
| DePaor1986_CirculatoryAutoregulation. |
Circulatory autregulation is the phenomenon whereby an isolated organ can maintain a constant or almost-constant blood flow rate over a range of perfusion pressures. A mathematical model is developed, based on work reported in the physiological literature, and tuned to show that autoregulation can be accomplished by pressure-induced oscillations in arteriolar radius. Various features known lo be exhibited by skeletal muscle and by stretch receptors are incorporated in the model of smooth muscle surrounding the arterioles. |
De Paor and Timmons, 1986 [33] |
Irrelevant | |
| Thiele2013 - Skeletal muscle myocytes. |
The model of skeletal muscle myocytes metabolism is derived from the community-driven global reconstruction of human metabolism (version 2.02, MODEL1109130000). |
Thiele et al., 2013 [34] |
Irrelevant | |
| Swainston2016 - Reconstruction of human metabolic network (Recon 2.2). |
Authors developed Recon 2.2, the most predictive model of human metabolism to date as demonstrated here. Extensive manual curation has increased the reconstruction size to 5324 metabolites, 7785 reactions and 1675 associated genes, which now are mapped to a single standard. The focus upon mass and charge balancing of all reactions, along with better representation of energy generation, has produced a flux model that correctly predicts ATP yield on different carbon sources. |
Swainston et al., 2016 [35] |
Irrelevant | |
| Duarte2007_Homo_sapiens_Metabol_Recon_1. |
Authors manually reconstructed the global human metabolic network based on Build 35 of the genome annotation and a comprehensive evaluation of >50 years of legacy data (i.e., bibliomic data). Herein they describe the reconstruction process and demonstrate how the resulting genome-scale (or global) network can be used (i) for the discovery of missing information, (ii) for the formulation of an in silico model, and (iii) as a structured context for analyzing high-throughput biological data sets. |
Duarte et al., 2007 [36] |
Irrelevant |
Table1. The result of search in BioModels database using query "skeletal muscle".
Conclusion
The model approaches discussed above address various spatial, temporal and biochemical resolutions and are conceptually complementary. However, they were not yet linked in an integrated computational framework and executed simultaneously using a modular approach (Snoep et al., 2006) [37] that has been implemented in BioUML platform. Computational modeling of metabolic responses of skeletal muscle to physiological stresses (e.g., hypoxia, ischemia, and exercise) is intended to quantitatively elucidate regulatory mechanisms. Although more detailed mechanisms can be included, these cannot be effectively validated without appropriate in vivo experimental data. With the availability of additional data, the model could incorporate and test alternative mechanisms of the regulation. The fact that available models do not account for blood flow heterogeneity and all fiber type distributions associated with skeletal muscle cellular metabolism constrains the application of virtual physiological modelling to sports or space travel.But the most significant limitation of the present models is that they do not account for detailed interconnetction between signaling pathways activated by physiological stresses and downstream changes on coupled transcriptional and metabolic levels using positive and negative feedbacks. In order to overcome these shortcomings, we are going to extend previously developed model (Li et al., 2009) [26] incorporating essential steps of AMPK signaling pathway in skeletal muscle which is regulated in a distinct manner during contraction depending on exercise intensity and duration.
References
- Janssen I, Heymsfield SB, Wang ZM, and Ross R. Skeletal muscle mass and distribution in 468 men and women aged 18-88 yr. J Appl Physiol (1985). 2000 Jul;89(1):81-8. DOI:10.1152/jappl.2000.89.1.81 |
- Kunz WS. Control of oxidative phosphorylation in skeletal muscle. Biochim Biophys Acta. 2001 Mar 1;1504(1):12-9. DOI:10.1016/s0005-2728(00)00235-8 |
- Gonzalez-Freire M, Semba RD, Ubaida-Mohien C, Fabbri E, Scalzo P, Højlund K, Dufresne C, Lyashkov A, and Ferrucci L. The Human Skeletal Muscle Proteome Project: a reappraisal of the current literature. J Cachexia Sarcopenia Muscle. 2017 Feb;8(1):5-18. DOI:10.1002/jcsm.12121 |
- Li Y, Lai N, Kirwan JP, and Saidel GM. Computational Model of Cellular Metabolic Dynamics in Skeletal Muscle Fibers during Moderate Intensity Exercise. Cell Mol Bioeng. 2012 Mar;5(1):92-112. DOI:10.1007/s12195-011-0210-y |
- Li Y, Solomon TP, Haus JM, Saidel GM, Cabrera ME, and Kirwan JP. Computational model of cellular metabolic dynamics: effect of insulin on glucose disposal in human skeletal muscle. Am J Physiol Endocrinol Metab. 2010 Jun;298(6):E1198-209. DOI:10.1152/ajpendo.00713.2009 |
- Korzeniewski B. Regulation of ATP supply during muscle contraction: theoretical studies. Biochem J. 1998 Mar 15;330 ( Pt 3)(Pt 3):1189-95. DOI:10.1042/bj3301189 |
- Korzeniewski B. Theoretical studies on how ATP supply meets ATP demand. Biochem Soc Trans. 1999 Feb;27(2):271-6. DOI:10.1042/bst0270271 |
- Lambeth MJ and Kushmerick MJ. A computational model for glycogenolysis in skeletal muscle. Ann Biomed Eng. 2002 Jun;30(6):808-27. DOI:10.1114/1.1492813 |
- Korzeniewski B and Liguzinski P. Theoretical studies on the regulation of anaerobic glycolysis and its influence on oxidative phosphorylation in skeletal muscle. Biophys Chem. 2004 Jul 1;110(1-2):147-69. DOI:10.1016/j.bpc.2004.01.011 |
- Cerretelli P, Pendergast D, Paganelli WC, and Rennie DW. Effects of specific muscle training on VO2 on-response and early blood lactate. J Appl Physiol Respir Environ Exerc Physiol. 1979 Oct;47(4):761-9. DOI:10.1152/jappl.1979.47.4.761 |
- Hughson RL, Tschakovsky ME, and Houston ME. Regulation of oxygen consumption at the onset of exercise. Exerc Sport Sci Rev. 2001 Jul;29(3):129-33. DOI:10.1097/00003677-200107000-00008 |
- Whipp BJ and Wasserman K. Oxygen uptake kinetics for various intensities of constant-load work. J Appl Physiol. 1972 Sep;33(3):351-6. DOI:10.1152/jappl.1972.33.3.351 |
- Mader A. Glycolysis and oxidative phosphorylation as a function of cytosolic phosphorylation state and power output of the muscle cell. Eur J Appl Physiol. 2003 Jan;88(4-5):317-38. DOI:10.1007/s00421-002-0676-3 |
- Vinnakota K, Kemp ML, and Kushmerick MJ. Dynamics of muscle glycogenolysis modeled with pH time course computation and pH-dependent reaction equilibria and enzyme kinetics. Biophys J. 2006 Aug 15;91(4):1264-87. DOI:10.1529/biophysj.105.073296 |
- Wu F, Jeneson JA, and Beard DA. Oxidative ATP synthesis in skeletal muscle is controlled by substrate feedback. Am J Physiol Cell Physiol. 2007 Jan;292(1):C115-24. DOI:10.1152/ajpcell.00237.2006 |
- Scopes RK. Studies with a reconstituted muscle glycolytic system. The rate and extent of creatine phosphorylation by anaerobic glycolysis. Biochem J. 1973 May;134(1):197-208. DOI:10.1042/bj1340197 |
- Beard DA. A biophysical model of the mitochondrial respiratory system and oxidative phosphorylation. PLoS Comput Biol. 2005 Sep;1(4):e36. DOI:10.1371/journal.pcbi.0010036 |
- Jeneson JA, van Dobbenburgh JO, van Echteld CJ, Lekkerkerk C, Janssen WJ, Dorland L, Berger R, and Brown TR. Experimental design of 31P MRS assessment of human forearm muscle function: restrictions imposed by functional anatomy. Magn Reson Med. 1993 Nov;30(5):634-40. DOI:10.1002/mrm.1910300515 |
- Zhou L, Salem JE, Saidel GM, Stanley WC, and Cabrera ME. Mechanistic model of cardiac energy metabolism predicts localization of glycolysis to cytosolic subdomain during ischemia. Am J Physiol Heart Circ Physiol. 2005 May;288(5):H2400-11. DOI:10.1152/ajpheart.01030.2004 |
- Zhou L, Stanley WC, Saidel GM, Yu X, and Cabrera ME. Regulation of lactate production at the onset of ischaemia is independent of mitochondrial NADH/NAD+: insights from in silico studies. J Physiol. 2005 Dec 15;569(Pt 3):925-37. DOI:10.1113/jphysiol.2005.093146 |
- Zhou L, Cabrera ME, Okere IC, Sharma N, and Stanley WC. Regulation of myocardial substrate metabolism during increased energy expenditure: insights from computational studies. Am J Physiol Heart Circ Physiol. 2006 Sep;291(3):H1036-46. DOI:10.1152/ajpheart.01382.2005 |
- Zhou L, Cabrera ME, Huang H, Yuan CL, Monika DK, Sharma N, Bian F, and Stanley WC. Parallel activation of mitochondrial oxidative metabolism with increased cardiac energy expenditure is not dependent on fatty acid oxidation in pigs. J Physiol. 2007 Mar 15;579(Pt 3):811-21. DOI:10.1113/jphysiol.2006.123828 |
- Dash RK, Dibella JA 2nd, and Cabrera ME. A computational model of skeletal muscle metabolism linking cellular adaptations induced by altered loading states to metabolic responses during exercise. Biomed Eng Online. 2007 Apr 20;6:14. DOI:10.1186/1475-925X-6-14 |
- Dash RK, Li Y, Kim J, Beard DA, Saidel GM, and Cabrera ME. Metabolic dynamics in skeletal muscle during acute reduction in blood flow and oxygen supply to mitochondria: in-silico studies using a multi-scale, top-down integrated model. PLoS One. 2008 Sep 9;3(9):e3168. DOI:10.1371/journal.pone.0003168 |
- Dash RK, Li Y, Kim J, Saidel GM, and Cabrera ME. Modeling cellular metabolism and energetics in skeletal muscle: large-scale parameter estimation and sensitivity analysis. IEEE Trans Biomed Eng. 2008 Apr;55(4):1298-318. DOI:10.1109/TBME.2007.913422 |
- Li Y, Dash RK, Kim J, Saidel GM, and Cabrera ME. Role of NADH/NAD+ transport activity and glycogen store on skeletal muscle energy metabolism during exercise: in silico studies. Am J Physiol Cell Physiol. 2009 Jan;296(1):C25-46. DOI:10.1152/ajpcell.00094.2008 |
- Zierath JR and Hawley JA. Skeletal muscle fiber type: influence on contractile and metabolic properties. PLoS Biol. 2004 Oct;2(10):e348. DOI:10.1371/journal.pbio.0020348 |
- Lai N, Camesasca M, Saidel GM, Dash RK, and Cabrera ME. Linking pulmonary oxygen uptake, muscle oxygen utilization and cellular metabolism during exercise. Ann Biomed Eng. 2007 Jun;35(6):956-69. DOI:10.1007/s10439-007-9271-4 |
- Lai M, Brun D, Edelstein SJ, and Le Novère N. Modulation of calmodulin lobes by different targets: an allosteric model with hemiconcerted conformational transitions. PLoS Comput Biol. 2015 Jan;11(1):e1004063. DOI:10.1371/journal.pcbi.1004063 |
- Shorten PR, O'Callaghan P, Davidson JB, and Soboleva TK. A mathematical model of fatigue in skeletal muscle force contraction. J Muscle Res Cell Motil. 2007;28(6):293-313. DOI:10.1007/s10974-007-9125-6 |
- Wu F, Yang F, Vinnakota KC, and Beard DA. Computer modeling of mitochondrial tricarboxylic acid cycle, oxidative phosphorylation, metabolite transport, and electrophysiology. J Biol Chem. 2007 Aug 24;282(34):24525-37. DOI:10.1074/jbc.M701024200 |
- Caron E, Ghosh S, Matsuoka Y, Ashton-Beaucage D, Therrien M, Lemieux S, Perreault C, Roux PP, and Kitano H. A comprehensive map of the mTOR signaling network. Mol Syst Biol. 2010 Dec 21;6:453. DOI:10.1038/msb.2010.108 |
- https://www.tandfonline.com/doi/abs/10.1080/00207178608933494
- Thiele I, Swainston N, Fleming RM, Hoppe A, Sahoo S, Aurich MK, Haraldsdottir H, Mo ML, Rolfsson O, Stobbe MD, Thorleifsson SG, Agren R, Bölling C, Bordel S, Chavali AK, Dobson P, Dunn WB, Endler L, Hala D, Hucka M, Hull D, Jameson D, Jamshidi N, Jonsson JJ, Juty N, Keating S, Nookaew I, Le Novère N, Malys N, Mazein A, Papin JA, Price ND, Selkov E Sr, Sigurdsson MI, Simeonidis E, Sonnenschein N, Smallbone K, Sorokin A, van Beek JH, Weichart D, Goryanin I, Nielsen J, Westerhoff HV, Kell DB, Mendes P, and Palsson BØ. A community-driven global reconstruction of human metabolism. Nat Biotechnol. 2013 May;31(5):419-25. DOI:10.1038/nbt.2488 |
- https://link.springer.com/article/10.1007%2Fs11306-016-1051-4
- Duarte NC, Becker SA, Jamshidi N, Thiele I, Mo ML, Vo TD, Srivas R, and Palsson BØ. Global reconstruction of the human metabolic network based on genomic and bibliomic data. Proc Natl Acad Sci U S A. 2007 Feb 6;104(6):1777-82. DOI:10.1073/pnas.0610772104 |
- Snoep JL, Bruggeman F, Olivier BG, and Westerhoff HV. Towards building the silicon cell: a modular approach. Biosystems. 2006 Feb-Mar;83(2-3):207-16. DOI:10.1016/j.biosystems.2005.07.006 |